Question

Locating Zeros of Polynomial Function:
Approximate the real zeros to the nearest tenth

Answer 1

we are given

`f(x)=2x^4-x^3+x-2`

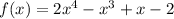
we can check each options

option-A:

-1,1

we can plug x=-1 and x=1 and check whethet f(x)=0

At x=-1:

`f(-1)=2(-1)^4-(-1)^3+(-1)-2`

`f(-1)=0`

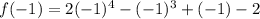
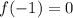
At x=1:

`f(1)=2(1)^4-(1)^3+(1)-2`

`f(1)=0`

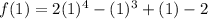
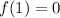
so, this is TRUE

option-B:

0,1

we can plug x=0 and x=1 and check whethet f(x)=0

At x=0:

`f(0)=2(0)^4-(0)^3+(0)-2`

`f(0)=-2`

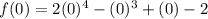
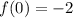
At x=1:

`f(1)=2(1)^4-(1)^3+(1)-2`

`f(1)=0`

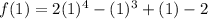
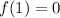
so, this is FALSE

option-C:

-2,-1

we can plug x=-2 and x=-1 and check whethet f(x)=0

At x=-2:

`f(-2)=2(-2)^4-(-2)^3+(-2)-2`

`f(-2)=36`

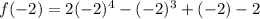
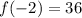
At x=-1:

`f(-1)=2(-1)^4-(-1)^3+(-1)-2`

`f(-1)=0`

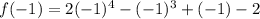
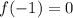
so, this is FALSE

option-D:

-1,0

we can plug x=-1 and x=0 and check whethet f(x)=0

At x=-1:

`f(-1)=2(-1)^4-(-1)^3+(-1)-2`

`f(-1)=0`

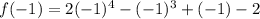
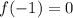
At x=0:

`f(0)=2(0)^4-(0)^3+(0)-2`

`f(0)=-2`

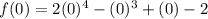
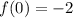
so, this is FALSE