Question

Dave can complete a sales route by himself in 4 hours. James can do the same job in 5 hours. How long will it take them to do it working together?

Answer 1

We can solve this problem by calculating the individual rate of working and equate it to their total rate of working.

If Dave can complete a sales route in 4 hours, then his working rate is


`(1)/(4)`

Also, if James can do it in 5 hours, then his working rate is


`(1)/(5)`

Let

`x`
be the hours that both will use to complete the sales route,

Then rate at which both completes this task is

`(1)/(x)`


Meaning if we add their individual rates we should get


`(1)/(x)`

That is;


`(1)/(4) + (1)/(5) = (1)/(x)`

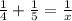
The LCM is

`20x`

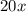
So let us multiply through with the LCM.


`20x * (1)/(4) + 20x * (1)/(5) =20x * (1)/(x)`


`5x + 4x = 20`

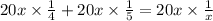
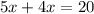
We simplify to get,


`9x = 20`

Dividing through by 9 gives;


`x = (20)/(9)`


`x = 2(1)/(9)`

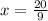
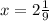
Therefore the two will complete sales route in

`2 (1)/(9)`
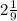
hours.