The student is incorrect. Although the amount of copper sulfate dissolved has increased in the new solution, we also have to account for the fact that the amount of water has also increased.
To see whether or not the new solution is more concentrated, we can compare the grams of copper sulfate in each solution to the amount of water in each solution.
Solution A:
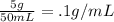
Solution B:
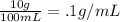
Solution A + Solution B:
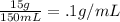
You'll notice that the concentration for all these solutions is .1 g copper sulfate/1mL
This means that the new solution (A+B) is not more concentrated -- the increase of dissolved copper sulfate was diluted by the additional increase of water, such that the concentration of the new solution was not greater than its component solutions (A and B).