Question

Please help, need answer fast!

Which expression is equivalent to (a^2b^4c)^2(6a^3b)(2c^5)^3/4a^6b^12c^3 ?

Answer 1

the answer is c. 12ac^14/b^3

Answer 2

The correct answer is C

`(12ac^(14))/(b^3)`

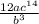
Explanation:

We want to simplify

`((a^2b^4c)^(2)(6a^3b)(2c^5)^3)/(4a^6b^(12)c^3)`.

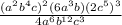Recall this property of exponents,

`(a^m)^n=a^(mn)`

When we apply this property our expression becomes,

`=((a^4b^8c^2)(6a^3b)(2^3c^15))/(4a^6b^(12)c^3)`.

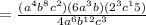We rearrange to get

`=(6*8* a^4* a^3 * b^8* b* c^2* c^(15))/(4a^6b^(12)c^3)`.

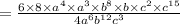We now apply another property of exponents to simplify the numerator.

According to this property,

`a^m* a^n=a^(m+n)`

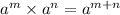
When we apply this property, the expression will now be,

`=(6*8* a^(4+3) * b^(8+1) c^(2+15))/(4a^6b^(12)c^3)`

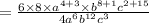
This simplifies to,

`=(48* a^(7) * b^(9) c^(17))/(4a^6b^(12)c^3)`

We again apply this property of exponents,

`(a^m)/(a^n)=a^(m-n)`.

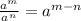When we apply this property, the expression will be,

`=12* a^(7-6) * b^(9-12) c^(17-3)`

`=12* a^1 * b^(-3) c^(14)`

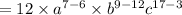
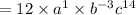
We rewrite this as a positive index to get,

`=(12ac^(14))/(b^3)`

The correct answer is C