Question

In the diagram abc=adb=90, ad=p and dc=q. Use similar triangles to show that x2=pz

plzz anyoneee

Answer 1

By comparing the ratios of sides in similar triangles ΔABC and ΔADB,we can say that
`x^(2) =pz`

Explanation:

Given that ∠ABC=∠ADC, AD=p and DC=q.

Let us take compare Δ ABC and Δ ADB in the attached file , ∠A is common in both triangles

and given ∠ABC=∠ADB=90°

Hence using AA postulate, ΔABC ≈ ΔADB.

Now we will equate respective side ratios in both triangles.

`(AB)/(AC)= (AD)/(AB)=(BD)/(BC)`

Since we don't know BD , BC let us take first equality and plugin the variables given in respective sides.

`(x)/(z)= (p)/(x)`

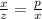
Cross multiply

`x^(2)=pz`

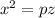
Hence proved.