Question

If you stand at the edge of a cliff that is 75 m high and throw a rock directly up into the air with a velocity of 20 m/s, at what time will the rock hit the ground? (note: the quadratic formula will give two answers, but only one of them is reasonable.)

Answer 1

At time 6.45 seconds rock will hit ground.

Step-by-step explanation:

We have equation of motion ,
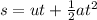`s= ut+(1)/(2) at^2`, s is the displacement, u is the initial velocity, a is the acceleration and t is the time.

Let us take up direction as positive, so displacement = -75 m, initial velocity = 20 m/s, acceleration = acceleration due to gravity = -9.8
`m/s^2`

Substituting

`-75= 20*t-(1)/(2) *9.8*t^2\\ \\ 4.9t^2-20t-75=0`

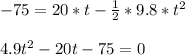
t = 6.45 seconds or t =-2.37 seconds

Since negative time is not possible, t = 6.45 seconds.

So at time 6.45 seconds rock will hit ground.

Answer 2

The vertical position of the rock is given by:

`y(t)=h+v_0 t -(1)/(2) gt^2`

where

h=75 m is the initial height

v0=20 m/s is the initial vertical velocity

g=9.81 m/s^2 is the acceleration due to gravity

The problem asks to find the time t at which the rock hits the ground, so the time t at which y(t)=0, so the equation above becomes:

`75 + 20 t - 4.9t^2 =0`

Which has two solutions:

t=-2.37 s

t=6.45 s

The first solution is a negative time so it has no physical meaning, therefore the correct answer is t=6.45 s.