Question

Can someone help me?

It's a class-8 maths .
Refer to the attachment.

Please don't spam and don't copy from web.
I need trusted answers and don't answer if you don't know.

Also i need it within 5 days as it will come in my exam.

Thank You!​

Answer 1

Explanation:

To start calculating, we first need to make some proof.

Firstly, since AB = AC, we know that ΔABC is isosceles, which means that ∠ABC = ∠ACB.

Now, looking only to ΔBDE and ΔCDF, we can see that they are similar, because the two of its angles are congruent:

∠BED=∠CFD

∠DBE=∠DCF

To make it easier to visualize which are the corresponding vertexes, we can draw them like this:

And we need to remember that BC is 24, so:

BD+CD=24

Since the triangles are similar, their corresponding sides have constant ratio, which we can calculate from the corresponding sides DE and CF:

`r=(CF)/(DE) =(7.5)/(4.5) =(5)/(3)`

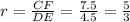
This ratio is the same for the other corresponding sides, so we can apply that for BD and CD:

`r=(CD)/(BD) =(5)/(3)\\ (BD)/(CD)=(3)/(5) \\\\ BD=(3)/(5) Cd`

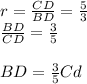
Thus, the measure of CF is approximately 13, alternative D.