First, let's convert the radical terms to exponents. Remember the following:
![\sqrt[n]{x^m} = x^(m)/(n)](https://img.qammunity.org/2019/formulas/mathematics/high-school/v3kewa9qs71kdwscp0mplga4q86ufjnuo9.png)
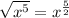
![\sqrt[4]{x^9} = x^{(9)/(4)}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/mm3a2i98h9it48fz4k5o4aebbz1xgeazce.png)
![\sqrt[6]{x^5} = x^{(5)/(6)}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/h05hg984960jtc8a9gruj535ppksxdwfhz.png)
After substituting in the values we just found, our expression looks like:
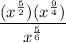
Now, remember that we can add the exponents of terms that have the same base and are being multiplied by each other. Also, remember that we can subtract the exponents of terms with the same base that are being divided by each other. This is represented as:
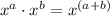
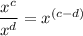
Thus, we can simplify our expression even more:
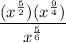
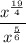
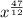
Our answer is
 .
.