We are given that
a and b are integers and 71 < ab < 76
We will check each options
option-A:
b=18
we can plug it
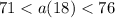
we can divide both sides by 18
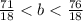
now, we can simplify it
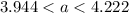
Since, 'a' is a integer
so, a=4 lies on interval
so, this interval is true
so, this is FALSE
option-B:
b=8
we can plug it
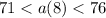
we can divide both sides by 8
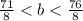
now, we can simplify it

Since, 'a' is a integer
so, a=9 lies on interval
so, this interval is true
so, this is FALSE
option-C:
b=12
we can plug it
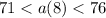
we can divide both sides by 12
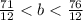
now, we can simplify it
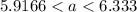
Since, 'a' is a integer
so, a=6 lies on interval
so, this interval is true
so, this is FALSE
option-D:
b=7
we can plug it
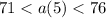
we can divide both sides by 7
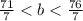
now, we can simplify it
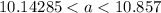
Since, 'a' is a integer
so, no integer lies on this interval
so, this interval is false
so, this is TRUE
option-E:
b=5
we can plug it
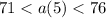
we can divide both sides by 5

now, we can simplify it

Since, 'a' is a integer
so, a=15
so, this interval is true
so, this is FALSE