Question

Solve the equation 9k2 – 6k = 11 by completing the square.

Answer 1

The answer to 9k2 – 6k = 11 is k = 11/12. Though, I'm not sure by the square part.

Here's the decimal form: k=0.91667

Steps:

Multiply the numbers. (9*2)

Add similar elements. (18k - 6k = 11)

Divide both sides by 12.

Simplify.

-

Hope this helped!

Answer 2

The solutions of the given equation are
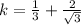`k=(1)/(3)+(2)/(√(3))` and
`k=(1)/(3)-(2)/(√(3))`.

Step-by-step explanation:

The given equation is

`9k^2-6k=11`

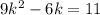
Divide both sides by 9.

`k^2-(2)/(3)k=(11)/(9)`

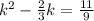
If an expression is
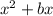`x^2+bx` then we need to add
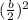`((b)/(2))^2` in the expression to make it perfect square.

In the above equation
`b=(2)/(3)`, so add
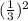`((1)/(3))^2` on both the sides.

`k^2-(2)/(3)k+((1)/(3))^2=(11)/(9)+((1)/(3))^2`

`(k-(1)/(3))^2=(11)/(9)+(1)/(9)`

`(k-(1)/(3))^2=(12)/(9)`

`(k-(1)/(3))^2=(4)/(3)`

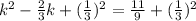
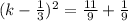
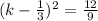
Taking square root both the sides.

`k-(1)/(3)=\pm \sqrt{(4)/(3)}`

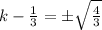
Add 1/3 on both the sides.

`k=(1)/(3)\pm (2)/(√(3))`

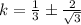
Therefore the solutions of the given equation are
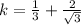`k=(1)/(3)+(2)/(√(3))` and
`k=(1)/(3)-(2)/(√(3))`.