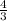Question

What is the roots of the quadratic equation? 6x^2+5x-4=0

Answer 1

x =
`(1)/(2)` or x = -
`(4)/(3)`

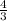
consider the factors of the product 6 × - 4 = - 24 which sum to the coefficient of the x- term ( + 5)

the factors are + 8 and - 3 ( split the middle term using these factors

6x² - 3x + 8x - 4 = 0 ( factor by grouping )

3x(2x - 1) + 4(2x - 1 ) ( take out common factor of (2x - 1) )

= (2x - 1)(3x + 4) = 0

equate each factor to zero and solve for x

2x - 1 = 0 ⇒ x =
`(1)/(2)`

3x + 4 = 0 ⇒ x = -
`(4)/(3)`

Answer 2

6x² + 5x - 4 = 0

Multiply the first and last term (6x² * -4) to get -24x². Now find two factors of -24x² whose sum is the middle term (5x). -3x + 8x Replace 5x with -3x + 8x, then factor and solve.

6x² - 3x + 8x - 4 = 0

3x(2x - 1) +4(2x - 1) = 0

(3x + 4) (2x - 1) = 0

3x + 4 = 0 or 2x - 1 = 0

x =
`-(4)/(3)` or x =
`(1)/(2)`

Note: you can also use the quadratic formula to find the foots.