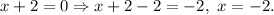Given:
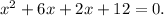
1. Combining like terms (here terms 6x and 2x both contain x, then we can combine them):
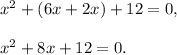
2. Distributive postulate:
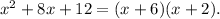
The equation is
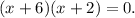
3. Zero product postulate (zero product postulate state that if a product of two factors is equal to zero, then first factor is equal to zero or second factor is equal to zero):
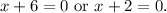
4. Subtraction property of equality:
a) subtract 6 from the first equation:

b) subtract 2 from the second equation: