Question

Use the identity (x2+y2)2=(x2−y2)2+(2xy)2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6.

Answer 1

let a,b be the two numbers. we know that a2-b2=5 and a*b=6

using the formula we are given

`(a^2+b^2)^2 = 5^2 + 12^2 = 169` we get the solution
`√(169) = 13`

Answer 2

13

Explanation:

Let x and y are two numbers. The difference of the squares if the two numbers is 5 and the product of the numbers is 6 such that,

`(x^2-y^2)=5`......................(1)

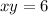`xy=6`..........(2)

We need to find the sum of the squares of two numbers. By using following identities it can be calculated as :

`(x^2+y^2)^2=(x^2-y^2)^2+(2xy)^2`

Using equation (1) and (2) in above equation, we get :

`(x^2+y^2)^2=5^2+(2* 6)^2`

`x^2+y^2=√(5^2+12^2)`

`x^2+y^2=13`

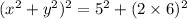
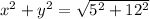
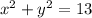
So, the sum of squares of two numbers is 13. Hence, this is the required solution.