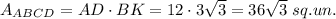Question

Given: ABCD ∥gram, BK ⊥ AD , AB ⊥ BD AB=6, AK=3 Find: m∠A, BK, AABCD

Answer 1

1. Consider right triangle ABK. The hypotenuse AB is 6 un. and the leg AK is 3 un. Since the leg is half of the hypotenuse, then the opposite to the leg angle is 30°. This means that m∠ABK=30°. Then m∠BAK=90°-30°=60°.

2. By the Pythagorean theorem,

`AB^2=AK^2+BK^2,\\\\6^2=3^2+BK^2,\\\\BK^2=36-9,\\\\BK^2=27,\\\\BK=3√(3)\ un.`

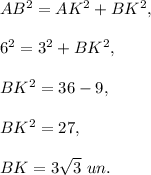
3. Consider right triangle ABD. In this triangle AD is hypotenuse and m∠ADB=90°-m∠BAD=90°-60°=30°. Then the leg AB opposite to the angle 30° is half of the hypotenuse and AD=12 un.

4. The area of parallelogram is

`A_(ABCD)=AD\cdot BK=12\cdot 3√(3)=36√(3)\ sq. un.`