Question

select whether the equation has a solution or not, square root x-2- square root 2x= square root x+2 (a. roots b. no roots)

Answer 1

The equation is
`\sqrt{x-2 \\ \\` -
`√(2x)` =
`√(x +2)`

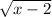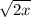Solution

Step 1:

Take square on both sides, we get

3x - 2
`√(x-2)`
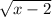
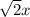`\sqrt2{x}` -2 = x +2

Step 2:

Subtract 3x - 2 from both sides, we get

-2
`√(x-2) √(2x) = -2x + 4`

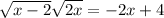
Step 3:

Again, square on both sides in order to get rid of the square root from the above equation, we get

`8x^(2)-16x = 4x^(2) -16x +16`

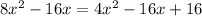
Now we have to simplify it,

`4x^(2) -16 = 0`

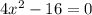
Step 4:

Now we have to solve this quadratic equation, in order to get the solution.

We get x = 2 and x = -2, When we verifying solution in the original given equation, the solution does not satisfy the equation.

Reason: We get negative number in the square root.

Therefore, it has no Roots.

Answer: b) No roots