Question

Need help asap please! Which equation matches the graph shown?

A.Y=x^2-6x+2
B.Y=2x^2-4x+2
C.Y=x^2-2x+1
D.Y=-2x^2+4x-2

Answer 1

The correct option is A.

Explanation:

The vertex form of a parabola is

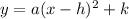`y=a(x-h)^2+k` ..... (1)

Where, (h,k) is vertex and a is a constant.

From the given graph it is clear that the vertex of the graph is (3,-7) and y-intercept is (0,2).

Substitute h=3 and k=-7 in equation (1).

`y=a(x-3)^2-7`

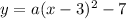
The y-intercept is (0,2). So, substitute c=0 and y=2 in the above equation to find the value of a.

`2=a(0-3)^2-7`

`2+7=a(3)^2`

`9=9a`

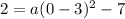
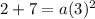
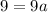
Divide both sides by 9.

`1=a`

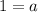
The value of a is 1.

Substitute a=1, h=3 and k=-7 in equation (1).

`y=1(x-3)^2-7`

`y=x^2-6x+9-7`

`y=x^2-6x+2`

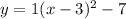
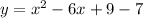
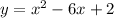
The equation of the parabola is
`y=x^2-6x+2`.

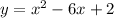Therefore the correct option is A.