Question

The vertices of triangle rst are r(–1,–2), s(2,–1), and t(4,2). If δjkl ∼ δrst and the length of kl is units , what is the length of jk?

Answer 1

sq root of 10 over 2

Explanation:

took it on edge

Answer 2

3.16 units

Explanation:

It has been given that the triangles JKL and the triangle RST are congruent.

That implies that, the length of the side JK, KL, and JL is equivalent to the length of the sides RS, ST, and RT respectively.

Now, to find the length of JK we need to find the length of the side RS. The coordinates of the points R and S are
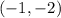`(-1,-2)` and
`(2,-1)`.

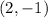The length of the side RS is equal to the distance between point R and S.

RS
`=√((x_2-x_1)^2+(y_2-y_1)^2)`

`= √((2-(-1))^2+(-1-(-(-2))^2)`

`=√(3^2+(-1+2)^2)`

`=√(9+1)=√(10)=3.16`

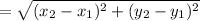
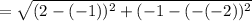
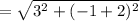
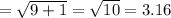
Now that we have the length of the side RS, and the triangles JKL and RST are congruent therefore, the length of the side JK is 3.16 units.