Question

Evaluate the limit ....

Answer 1

It depends on how t is approaching 2.

In fact, if you consider the right limit, you have

`\displaystyle \lim_(t \to 2^+) (2-t)/(|t-2|)`

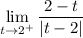
But since t is greater than 2, t-2 is positive, and thus |t-2| = t-2.

So, the limit becomes

`\displaystyle \lim_(t \to 2^+) (2-t)/(t-2) = \lim_(t \to 2^+) -1 = -1`

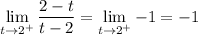
On the other hand, if you consider the left limit, you have

`\displaystyle \lim_(t \to 2^-) (2-t)/(|t-2|)`

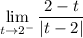
But since t is less than 2, t-2 is negative, and thus |t-2| = -t+2.

So, the limit becomes

`\displaystyle \lim_(t \to 2^+) (2-t)/(-t+2) = \lim_(t \to 2^+) 1 = 1`

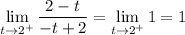
So, this limit does not exist, because the left and right limits exist but are not the same.