Given : Invested amount = $5000.
Rate of interet = r% compunded monthly.
Number of years = 4 years.
Total interest received = $1866.
Therefore, total amount after 4 years = 5000+1866 = $6866.
We know, formula for compound interest :
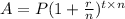 , where P is the invested amount, n is the number of monthly installments in an year.
, where P is the invested amount, n is the number of monthly installments in an year.
Number of months in an year are 12.
Plugging n=12, P=5000, t=4 in the formula now, we get
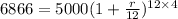

Dividing both sides by 5000, we get
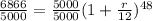

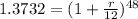
Taking 48th root on both sides, we get
![\sqrt[48]{1.3732} = \sqrt[48]{(1+(r)/(12))^(48)}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/boxfpo9lniedje6pks3kk4k1nh7tkz3hrb.png)
![\sqrt[48]{1.3732}=\left(1+(r)/(12)\right)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/vtokmhmcsbexs4g2h8cwnbkj478v5w343e.png)
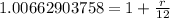
Subtracting 1 from both sides, we get
0.00662903758 =
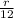
Multiplying by 12 on both sides, we get
r=0.07954845101
r≈0.0795
Or 7.95%.
A) The value of r is 7.95% compounded monthly.
Now, we need to find the interest after four years if the rate of interest is 3.6% compounded quarterly.
There are 4 quarters in an year.
So, n=4 and r=3.6%= 0.036.
Plugging values in compound interest formula now, we get

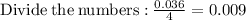
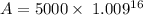

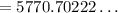
A≈5770.70
Subtracting 5770.70 -5000.00 = 770.70.
B) Therefore, the total interest he received at the end of the four years upto two decimal places is $770.70.