Question

Use the identity (x+y)(x2−xy+y2)=x3+y3 to find the sum of two numbers if the product of the numbers is 10, the sum of the squares of the numbers is 29, and the sum of the cubes of the numbers is 133.

Answer 1

Solve the given expression for the sum of the two numbers:

`x+y = (x^3+y^3)/(x^2-xy+y^2)`

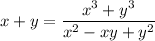
which you can rewrite as

`x+y = (x^3+y^3)/(x^2+y^2-xy)`

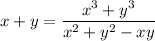
Now, we are given the product of the numbers (i.e. xy) to be 10, the sum of the squares of the numbers (i.e.
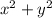`x^2+y^2`) to be 29, and the sum of the cubes of the numbers (i.e.
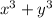`x^3+y^3`) to be 133.

If we plug these values in the formula written above, we have

`x+y = (133)/(29-10) = (133)/(19) = 7`