Question

The area of a rectangle is 45 ft2. If the length of the long side of the rectangle is 80% greater than the short side of the rectangle, what is the length of the longer side?

Answer 1

The area of a rectangle is 45 ft^2

If the length of the long side of the rectangle is 80% greater than the short side of the rectangle.

Let the shortest side be the width (x)

Length of rectangle L = 80% greater than x

So length = 0.8 x + x

Length = 1.8 x

Area of the rectangle = Length * width

45 = 1.8x * x

`45= 1.8x^2`

Divide by 1.8 from both sides'

`25= x^2`

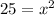
Take square root on both sides

x=5

so width of the rectangle = 5 feet

Length of the rectangle (longer side) = 1.8x = 1.8 * 5 = 9 feet

Answer 2

To solve this problem we propose the following equation:

1)
`b*h =45\\` This is the equation of the area of a rectangle.

Where a and b are the sides of the rectangle

If b is the longest side, then

b is 80% longer than h.

2)
`b= h+0.8h\\`

Now we have 2 equations and two unknowns.

Therefore we solve the following equations

`45=b*(b)/(1+0.8)\\`

`b^2=45(1+0.8)`

`b =√(45(1+0.8))\\`

b = 9 feet

The length of the longest side is 9 feet.