Question

What you s the distance between (13,-6) and (13,12) on the coordinate plane?

Answer 1

To find the distance, you would use the distance formula, which is:

`\sqrt{(x2 - x1)^(2) + (y2 - y1)^(2)}`

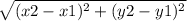
But, in this case, both of the x values are 13, meaning we can cancel out the x values (or just subtract y₁ from y₂, to get the distance ):

`\sqrt{(13 - 13)^(2) + (y2 - y1)^(2)}`

`\sqrt{(0)^(2) + (y2 - y1)^(2)}`

`\sqrt{0 + (y2 - y1)^(2)}`

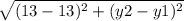
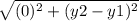
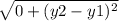
Because of this, we only need to find the distance between y₁ and y₂. Plug in the -6 and 12:

`\sqrt{(12 + 6)^(2)}` Plug in both y terms.

`\sqrt{18^(2)}` Simplify as much as possible.

= 18 The √ and the ² cancel out.

Therefore, the distance between (13, -6) and (13, 12) is 18.

Hope this helps! :)

EDIT: all the subscripts and most of the exponents showed up incorrectly. should be fixed now.

Answer 2

since both x values are the same and since the y values are 18 digits apart, the distance between both points is 18 units.