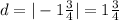To get the distance between
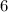 and
and
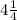 , we subtract
, we subtract
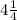 from
from
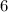
That is,
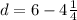
We change the mixed number to improper fraction now to get,
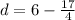
This is the same as,
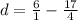
We collect LCM to be 4
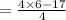
This gives us,
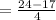
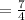
Convert back to mixed number to get,
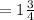
Therefore the distance between the two numbers is
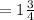
Note that the other way round will result in negative value. That is subtracting 6 from
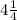 will give
will give
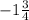
But since this is distance we find the absolute value and get the same result.