Answer:
The florist should make 9 Easter bouquet and 6 Spring bouquet to maximize the profit.
Explanation:
Suppose, the number of the Easter bouquet is
 and the number of Spring bouquet is
and the number of Spring bouquet is
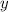 .
.
The Easter bouquet requires 10 jonquils and 20 daisies, and the Spring bouquet requires 5 jonquils and 20 daisies.
So, the total number of jonquils required
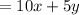
and the total number of daisies required
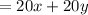
Given that, there are total 120 jonquils and 300 daisies are available. So, the constraints will be........
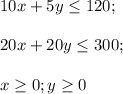
(As the number of each type of bouquet can't be negative)
Now, each Easter bouquet produces a profit of $1.50 and each Spring bouquet produces a profit of $1. So, the profit function will be:
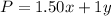
If we graph the constraints now, then the vertices of the common shaded region are:
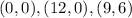 and
and
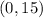
For (0, 0) ⇒
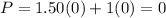
For (12, 0) ⇒
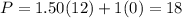
For (9, 6) ⇒
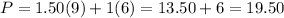
For (0, 15) ⇒
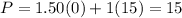
So, the profit will be maximum when
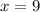 and
and
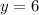
Thus, the florist should make 9 Easter bouquet and 6 Spring bouquet to maximize the profit.