Question

If f(x) = 3x and g(x) = 1/3x which expression could be used to verify that g(x) is the inverse of f(x)?

A. 3x(x/3)
B. (1/3x)(3x)
C.1/3(3x)
D. 1/3(1/3x)

Answer 1

If we want to verify that g ( x ) is the inverse of f ( x ) we have to show that:

( f ° g ) = ( g ° f )

f ( g ( x ) )= 3 · ( 1/3 x ) = x

g ( f ( x ) ) = 1/3 · ( 3 x ) = x

Answer:

C ) 1/3 ( 3 x )

Answer 2

C. 1/3(3x)

Explanation:

To verify if two functions are inverse, we have to find the composition of such functions, that is:

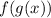`f(g(x))`; which results must be the variable
`x` to be inverse functions.

We know that:
`f(x)=3x;g(x)=(1)/(3)x`.

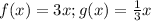Replacing on the composition:

`f(g(x))=3((1)/(3)x)=x`

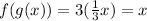
Therefore, the expression that has to be used to verify that these functions are inverse is C.