Can someone explain this differentiation question to me? I can differentiate but then I'm not sure what I am doing

Question

asked May 20, 2019 92.9k views

1 Answer

Jonah Graham · Answer 1 · 2019-05-24T22:43:37+0000

note that gradient =
(dy)/(dx) at x = a

calculate
(dy)/(dx) for each pair of functions and compare gradient

(a)

(dy)/(dx) = 2x and
= - 1

at x = 4 : gradient = 8 and - 1 : 8 > - 1

(b)

(dy)/(dx) = 2x + 3 and
= - 2

at x = 2 : gradient = 7 and - 2 and 7 > - 2

(c)

(dy)/(dx) = 4x + 13 and
= 2

at x = - 7 : gradient = - 15 and 2 and 2 > - 15

(d)

(dy)/(dx) = 6x - 5 and
= 2x - 2

at x = - 1 : gradient = - 11 and - 4 and - 4 > - 11

(e)

y = √x =
$x^{(1)/(2) }$

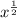
(dy)/(dx) = 1/(2√x) and
= 2

at x = 9 : gradient =
(1)/(6) and 2 and 2 >
(1)/(6)