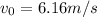The problem corresponds to the motion of a projectile (the salmon), with initial speed
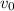 , initial direction
, initial direction
 and vertical acceleration
and vertical acceleration
 downward. The two equations which gives the horizontal and vertical position of the salmon at time t are
downward. The two equations which gives the horizontal and vertical position of the salmon at time t are
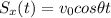 (1)
(1)
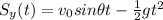 (2)
(2)
We can solve the problem by requiring Sx=3.16 m and Sy=0.379 m, the data of the problem.
Solving eq.(1) for t:
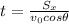
And substituting this expression of t into eq.(2), we get the following expression for
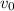 :
:

And substituting the numbers into the equation, we find