Question

Simplify the expression. 12x^-6 y^10 times 3x^7 y

Answer 1

We need to simplify the expression:

`12x^(-6)y^(10) * (3x^(7)y)`

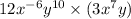
Now, we know that we can resolve the exponents of the variables with the like terms only and we can multiply the coefficients independently:

Now,

`12x^(-6)y^(10) * 3x^(7)y=(12 * 3)* (x^(-6)* x^(7))* (y^(10)* y)`

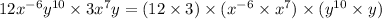
On simplifying the above expression we get:

`36* x^((-6+7))* y^((10+1))`

`=36 * x^(1)* y^(11)`

`=36 * x * y^(11)`

`=36xy^(11)`

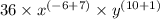
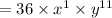
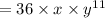
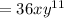
So the simplified form of the expression
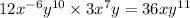`12x^(-6)y^(10) * 3x^(7)y=36xy^(11)`.