Solution:- Let f and g be the functions such that
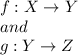
can be used to form a function which maps x in X to
 in Z.
in Z.
If z is a function of y, and y is a function of x, then z is a function of x. (transitive property)
Hence the composite function is given by
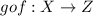 , defined by
, defined by
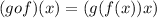 for x in X.
for x in X.
Now , for the function g(x) into the function for f(x), we have to work from the inside out by substituting the expression. So by this way composition of function related to order of operations.