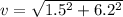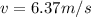Question

A ferry approaches shore, moving north with a speed of 6.2 m/s relative to the dock. A person on the ferry walks from one side of the ferry to the other, moving east with a speed of 1.5 m/s relative to the ferry. What is the speed of the person relative to the dock?

Answer 1

Speed of Ferry is towards North with magnitude 6.2 m/s

Here if we assume that North direction is along Y axis and East is along X axis then we can say

`\vec v_f = 6.2 \hat j`

Now a person walk on ferry with speed 1.5 m/s towards east with respect to Ferry

so it is given as

`\vec v_(pf) = 1.5 \hat i`

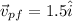
also by the concept of relative motion we know that

`\vec v_(pf) = \vec v_p - \vec v_f`

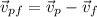
now plug in all values in it

`1.5 \hat i = \vec v_p - 6.2 \hat j`

`\vec v_p = 1.5 \hat i + 6.2 \hat j`

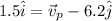
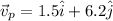
now if we need to find the speed of the person then we need to find its magnitude

so it is given as

`v = √(1.5^2 + 6.2^2)`

`v = 6.37 m/s`