Question

Line segments JK and JL in the xy-coordinate plane both have a common endpoint J(-4,11) and midpoints at M, (2, 16) and M2 (-3,5), respectively. What is the distance between M, and M2? Round to the nearest tenth.

Answer 1

12.1

Explanation:

We use the formula for the distance between two arbitrary points
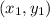`(x_1,y_1)` and
`(x_2,y_2)` in the xy-coordinate plane, that is:

`d=√((x_1-x_2)^2 + (y_1-y_2)^2)`

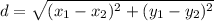
So, replacing the points
`M=(2,16)` and
`M_2=(-3,5)`, we obtain:

`d=√((2-(-3))^2 + (16-5)^2)\\d=√((2+3)^2 + (16-5)^2)\\d=√(5^2 + 11^2)\\d=√(146 )=12.083045... \simeq 12.1`

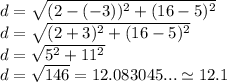
that is the answer.

note: observe that we only use the coordinates between the two midpoints and not the point J.