Question

To travel 100 miles, it takes Sue, riding a moped, 3 hours less time than it takes Doreen to travel 42 miles riding a bicycle. Sue travels 19 miles per hour faster than Doreen. Find the times and rates of both girls.

Answer 1

Let us assume Doreen rate = x miles per hour.

Sue travels 19 miles per hour faster than Doreen.

Therefore,

Rate of Sue = (x+19) miles per hour.

We know time, rate and distance relation as

Time = Distance / rate.

Therefore, time taken by Doreen to travel 42 miles at the rate x miles per hour =

`(42)/(x)`.

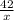And time taken by Sue to travel 100 miles at the rate (x+19) miles per hour =

`(100)/((x+19))`.

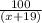Sue takes 3 hours less time than it takes Doreen.

Therefore,

`(42)/(x)-(100)/((x+19))=3`

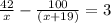
We need to solve the equatuion for x now.

`(42)/(x)-(100)/(\left(x+19\right))=3`

`\mathrm{Find\:Least\:Common\:Multiplier\:of\:}x,\:x+19:\quad x\left(x+19\right)`

`\mathrm{Multiply\:by\:LCM=}x\left(x+19\right)`

`(42)/(x)x\left(x+19\right)-(100)/(x+19)x\left(x+19\right)=3x\left(x+19\right)`

`42\left(x+19\right)-100x=3x\left(x+19\right)`

`-58x+798=3x^2+57x`

`3x^2+57x=-58x+798`

`3x^2+57x-798=-58x+798-798`

`3x^2+57x-798=-58x`

`\mathrm{Add\:}58x\mathrm{\:to\:both\:sides}`

`3x^2+57x-798+58x=-58x+58x`

`3x^2+115x-798=0`

`\mathrm{Solve\:with\:the\:quadratic\:formula}`

`\quad x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

`x=(-115+√(115^2-4\cdot \:3\left(-798\right)))/(2\cdot \:3):\quad 6`

`x=(-115-√(115^2-4\cdot \:3\left(-798\right)))/(2\cdot \:3):\quad -(133)/(3)`

`x=6,\:x=-(133)/(3)`

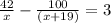
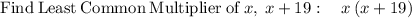
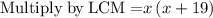
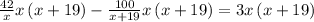
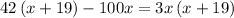
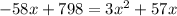
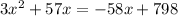
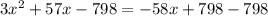
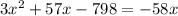
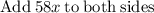
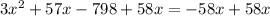
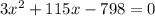
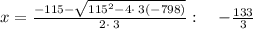
We can't take rates as negative numbers.

So, the rate of Doreen (x) = 6 miles per hour.

Rate of Sue = x+19 = 6+19 = 25 miles per hour.

Time taken by Doreen @ 6 miles per hour to cover 42 miles = 42/6 = 7 hours.

Time taken by Sue @ the rate 25 miles per hour to cover 100 miles = 100/25 = 4 hours.