Question

Help!! What is the point in the feasible region maximizes the objection function?

Answer 1

First, find the vertices of the shaded region. You can do this my graphing or by solving a system of equations for each pair of functions. I am going to find them by graphing.

x ≥ 0 and y ≥ 0 place the shaded region in the first quadrant with a vertex at (0, 0)

now graph y ≤ 3. a vertex is at (0, 3)

now graph y < -2x + 5. a vertex is at (1, 3). the other vertex is the x-intercept (when y = 0).

0 = -2x + 5

-5 = -2x

`(5)/(2) = x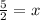` So, the vertex is
`((5)/(2) , 0)`

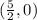
Next, input the coordinates of the vertices into the objective function.

C = -6x + 5y

(0, 0): C = -6(0) + 5(0)

= 0 + 0

= 0

(0, 3): C = -6(0) + 5(3)

= 0 + 15

= 15

(1, 3): C = -6(1) + 5(3)

= -6 + 15

= 9

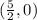`((5)/(2) , 0)`: C = -6(\frac{5}{2}[/tex]) + 5(2)

= -15 + 10

= -5

The maximum is C = 15 which occurs at vertex (0, 3)

Answer: A