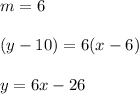Question

A line passes through the points (6, 10) and (4, -2).

(a) Find the slope of the line. Show all your work.

(b) Write the equation of the line in point-slope form. Show all your work

(c) Write the equation of the line in slope-intercept form. Show all your work

Answer 1

For this case we have:

Part A:

Point 1:
`(x1, y1) = (6,10)\\`

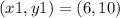
Point 2:
`(x2, y2) = (4, -2)\\`

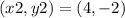
We know that the slope m is given by:

`m = ((y2-y1))/((x2-x1))\\\\m = ((- 2-10))/((4-6))\\\\m = ((- 12))/((- 2))\\`

`m = 6\\`

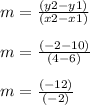
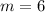
The slope is
`m = 6\\`

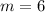
Part b:

The equation of the line in point-slope form is given by:

`(y-y1) = m (x-x1)\\`

Substituting the point 1
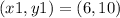`(x1, y1) = (6,10)`we have:

`(y-10) = 6 (x-6)\\`

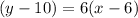
Thus, the point-slope equation is:
`(y-10) = 6 (x-6)\\`

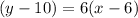
Part c:

The equation of the line in slope-intersection form is given by:

`y = mx + b\\`

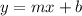
Rewriting the equation of part b we have:

`y = 6 (x-6) +10\\\\y = 6x-36 + 10\\\\y = 6x-26\\`

Thus, the equation of the line in slope-intersection form is

`y = 6x-26\\`

Answer:

`m = 6\\\\(y-10) = 6 (x-6)\\\\y = 6x-26`