Here we need to find the average rate of change of
 .
.
Now,
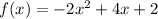
Let us find out the value of
 at the point
at the point
 .
.
Plugging
 in the equation we get:
in the equation we get:
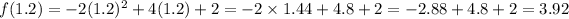
So,
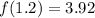
Now calculating the value of
 at
at
 .
.

So,

Now that we have the values of the function at two distinct points, we can find the average by using the formula given below:
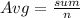 , where 'n' represents the number of values and that is two in our case and sum represents the sum of the values of the function.
, where 'n' represents the number of values and that is two in our case and sum represents the sum of the values of the function.
Therefore,

So, the average rate of change of the function
 from 1.2 to 3.8 is
from 1.2 to 3.8 is
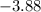 .
.