Question

An isosceles triangle has angle measures of (2x degrees) and (5x degrees). What are three possible angle measures of the triangle? Show all work.

Answer 1

100, 40, 40

Explanation:

First, do 2x+2x+5x because an isosceles triangle has two equal angles. We know that a triangle's total angle is 180 degrees so we do 180/9=20 x=20. Then multiply 2 by 20 to get 40. Then multiply 5 by 20 to get 100. So you get 40 40 100.

Answer 2

`40^(\circ),\:40^(\circ),\: 100^(\circ)`

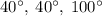
Explanation:

The interior angles of any triangle always add up to
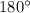`180^(\circ)`. In an isosceles triangle, (at least) two sides are congruent and therefore their base angles are also congruent. We can then form the following equation:

`2x+2x+5x=180`, where
`x` is some constant.

Solving, we get:

`9x=180,\\x=20`

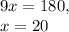
Therefore, plugging our constant back in, our angles are:

`2(20),\: 2(20), \: 5(20), \\\fbox{$40^(\circ),\:40^(\circ),\: 100^(\circ)$}`.

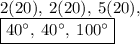Note this is only one group of possible angles. We could've also set the angle represented by
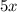`5x` to be the pair of angles that are congruent, and depending on your definition of isosceles, each angle measure could be
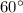`60^(\circ)` (equilateral).