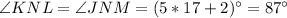Answer:
The measure of
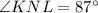
Explanation:
According to the below diagram, horizontal line segment
 intersects with
intersects with
 at their midpoint
at their midpoint
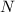 .
.
So,
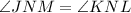 (As they are vertical angles)
(As they are vertical angles)
Given that,
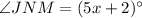 and
and
![\angle MNL = [3(x+14)]\°](https://img.qammunity.org/2019/formulas/mathematics/middle-school/i3ctzf7zyjvbo98ogs09f3ap3e2jjpqcez.png)
As they are adjacent angles and points
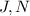 and
and
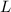 are co-linear, so
are co-linear, so
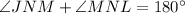
That means.......
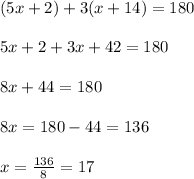
Thus,