Question

Help. I need help with these questions ( see image).
Please show workings.

Answer 1

9514 1404 393

Answer:

4) 6x

5) 2x +3

Explanation:

We can work both these problems at once by finding an applicable rule.

`\text{For $f(x)=ax^n$}\\\\\lim\limits_(h\to 0)(f(x+h)-f(x))/(h)=\lim\limits_(h\to 0)(a(x+h)^n-ax^n)/(h)\\\\=\lim\limits_(h\to 0)(ax^n+anx^(n-1)h+O(h^2)-ax^n)/(h)=\boxed{anx^(n-1)}`

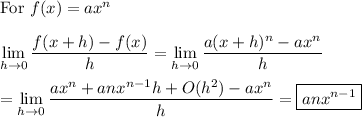
where O(h²) is the series of terms involving h² and higher powers. When divided by h, each term has h as a multiplier, so the series sums to zero when h approaches zero. Of course, if n < 2, there are no O(h²) terms in the expansion, so that can be ignored.

This can be referred to as the power rule.

Note that for the quadratic f(x) = ax^2 +bx +c, the limit of the sum is the sum of the limits, so this applies to the terms individually:

lim[h→0](f(x+h)-f(x))/h = 2ax +b

__

4. The gradient of 3x^2 is 3(2)x^(2-1) = 6x.

5. The gradient of x^2 +3x +1 is 2x +3.

__

If you need to "show work" for these problems individually, use the appropriate values for 'a' and 'n' in the above derivation of the power rule.