Question

assume that when adults with smartphones are randomly selected, 44% use them in meetings or classes. If 10 adult smartphones users are randomly selected find the probability that fewer than 3 of them

Answer 1

Solution: The given random experiment follows Binomial distribution with
`n=10,p=0.44`

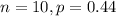
Let
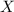`X` be the number of adults who use their smartphones in meetings or classes.

Therefore, we have to find:

`P(X<3)`

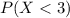
We know the binomial model is:

`P(X=x)=\binom{n}{x} p^(x) (1-p)^(n-x)`

`\therefore P(X<3) = P(X=0)+P(X=1) +P(X=2)`

`=\binom{10}{0}0.44^(0)(1-0.44)^(12-0)+\binom{10}{1}0.44^(1)(1-0.44)^(10-1)+\binom{10}{2}0.44^(2)(1-0.44)^(10-2)`

`=1 * 1 * 0.0030 + 10 * 0.44 * 0.0054 + 45 * 0.1936 * 0.009672`

`=0.0030+0.0238+0.0843`

`=0.1111`

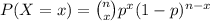
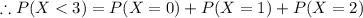
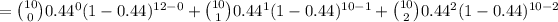
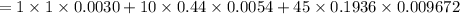
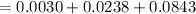
Therefore, the probability that fewer than 3 of them is 0.1111