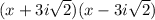Factor the expression over the complex numbers. x^(2) +18

Question

Factor the expression over the complex numbers.


`x^(2) +18`

Answer 1

`(x+3i√(2))(x-3i√(2))`

Explanation:

1. You must apply the Quadratic formula, which is:

`x=\frac{-b+/-\sqrt{b^(2)-4ac} }{2a}`

2. Substitute values:

`a=1\\b=0\\c=18`

`x=\frac{-0+/-\sqrt{0^(2)-4(1)(18)} }{2(1)}\\x=(+/-√(-72))/(2)\\x=(+/-6i√(2))/(2)\\x=+/-3i√(2)`

3. Finally, you obtain:

`(x+3i√(2))(x-3i√(2))`

Answer 2

Here we are given the expression:

`x^(2)+18`

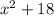
Now let us equate it to zero to find x first,

`x^(2)+18=0`

Now subtracting 18 from the other side,

`x^(2)=-18`

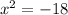
taking square root on both sides,

So we will get two values of x as ,

`x=3√(-2)`

`x=-3√(-2)`

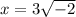
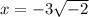
Now we can write square root -1 as i,

So our factors become,

`x=3i√(2)`

`x=-3i√(2)`

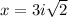
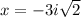
Answer:

The final factored form becomes,

`(x+3i√(2))(x-3i√(2))`