Question

A particle moving along the x axis so that it’s position at t is greater than or equal to 0 is given by s(t)=(t)ln(3t). Find the acceleration of the particle when the velocity is first zero.

Answer 1

We are given

equation of position

`s(t)=(t)ln(3t)`

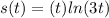
Calculation of velocity:

we can find derivative

`s'(t)=1*ln(3t)+t*(3)/(3t)`

`s'(t)=ln(3t)+1`

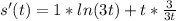
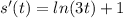
so, velocity is

`v(t)=ln(3t)+1`

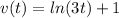
now, we can set it to 0

and then we can solve for t

`v(t)=ln(3t)+1=0`

`t=(1)/(3e)`

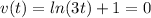
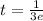
Calculation of acceleration:

we can find derivative again

`v'(t)=(3)/(3t) +0`

`v'(t)=(1)/(t)`

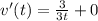
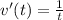
so, acceleration is

`a(t)=(1)/(t)`

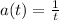
now, we can plug value of t

`a((1)/(3e))=(1)/((1)/(3e))`

`a((1)/(3e))=3e`..................Answer