Question

The height, in feet, of an arrow shot from a bow in an upwards direction, is modeled by the function h(t) = -16t2 + 96t + 5, where t represents the time in minutes.

Answer 1

Given function: h(t) = -16t^2 + 96t + 5, where t represents the time in minutes.

We need to find the interval for which the arrow is going up.

The arrow is going up would be the values of time t =0 when it start and when it went to highest point.

Given function is a quadratic function and it represents a parabolic shape.

The highest point on the parabola is a vertex point.

Therefore, we need to find the x-coordinate of the vertex.

We know, formula for x-coordinate of the vertex is

`(-b)/(2a)`

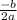
For the given quadratic a= -16 and b=96.

Plugging values of a and b in formula, we get

`(-96)/(2(-16))=(-96)/(-32) = 3.`

Therefore, after 3 seconds arrow would be at maximum height.

Therefore, the interval for which the arrow is going up is [0,3].