Answer: D. 0.29 m
Step-by-step explanation:
We will use the following equations to describe the leap of the cat:
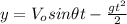 (1)
(1)
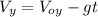 (2)
(2)
Where:
 is the height of the cat
is the height of the cat
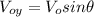 is the cat's initial velocity
is the cat's initial velocity
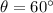
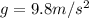 is the acceleration due gravity
is the acceleration due gravity
 is the time
is the time
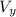 is the y-component of the velocity
is the y-component of the velocity
Now the cat will have its maximum height
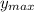 when
when
 . So equation (2) is rewritten as:
. So equation (2) is rewritten as:
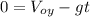 (3)
(3)
Finding
 :
:
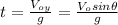 (4)
(4)
 (5)
(5)
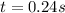 (6)
(6)
Substituting (6) in (1):
 (7)
(7)
Finally:
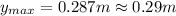 (8)
(8)