Question

*EASY POINTS!*

How many times larger is 6 × 10^10 than 2 × 10^-3?
(Its an exponent question!)

Answer 1

If you need to, you can write and solve an equation for the factor you seek.

... 6×10^10 = factor × 2×10^-3

Divide by 2×10^-3 to find the value of the factor:

... (6×10^10)/(2×10^-3) = factor

... factor = (6/2)×10^(10-(-3))

... factor = 3×10^13

The first number is 3×10^13 times the second number.

_____

An exponent signifies repeated multiplication.

... 10×10×10 = 10³

Just as you cancel common factors when you do division, you can subtract exponents.

`(10\cdot 10\cdot 10)/(10\cdot 10)=(10)/(1)=10\\\\(10^3)/(10^2)=10^(3-2)=10^1=10`

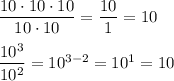
The same process works regardless of the signs of the exponents. When multiplying, we add exponents; when dividing we subtract the exponent of the denominator.