Question

The average income, I, in dollars, of a lawyer with an age of x years is modeled with the following function: I = -425x^2 + 45,500x – 650,000.

What is the youngest age for which the average income of a lawyer is $275,000? Round to the nearest year.

According to this model, what is the predicted average annual income of 40-year-old lawyers? Round to the nearest whole dollar.

Answer 1

We are given

The average income, I, in dollars is

`I=-425x^2+45500x-650000`

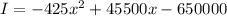
(a)

now, we are given

average income is $275000

so,
`I=275000`

now, we can set them equal

and then we can solve for x

`275000=-425x^2+45500x-650000`

`-425x^2+45500x-925000=0`

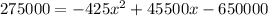
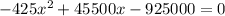
we will have to use quadratic formula

`x=(-45500+√(45500^2-4\left(-425\right)\left(-925000\right)))/(2\left(-425\right)):\quad (-√(45500^2-1572500000)+45500)/(850)`

`x=(-45500-√(45500^2-4\left(-425\right)\left(-925000\right)))/(2\left(-425\right)):\quad (√(45500^2-1572500000)+45500)/(850)`

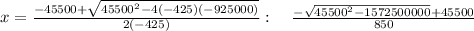
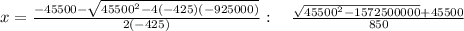
we get

`x=27.28199`

`x=79.776`

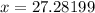
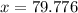
we need to find youngest age

It means that we need to choose smallest value

so,

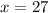`x=27`............Answer

(b)

we are given

x=40

so, we can plug it and find I

`I=-425(40)^2+45500(40)-650000`

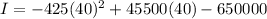
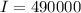`I=490000`..............Answer