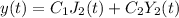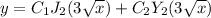Answer:
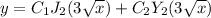
Explanation:
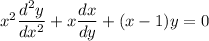
Considering
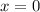 ordinary point we could use Frobenius method assuming
ordinary point we could use Frobenius method assuming
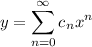
and consider the series representation given by the method to solve the equation. I think this way is harder.
In your case, It seems to have something to do with Bessel differential equation
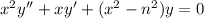
that will have the same representation as the Frobenius method. To get the form
 as we have
as we have
 in the given equation we can substitute
in the given equation we can substitute
 and take
and take
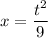
Thus,
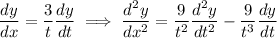
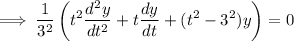
The solution will have the format
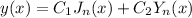
such that
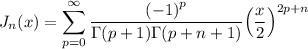
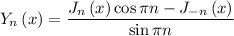
and
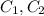 are constants
are constants
And the order of the Bessel equation is
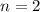
In our case, we can just write