Answer:
Option C.
Explanation:
The given function is

where x represents the number of minutes the painter has worked from the 100-minute mark through the 200-minute mark of the project.
We need to find the practical range of the function.
The value of x lies from 100 to 200.
At x=100,
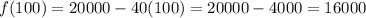
At x=200,

It means the practical range of the function is all real numbers between 12,000 and 16,000 inclusive.
Hence, the correct option is C.