Question

A rectangle is placed inside a circle whose diameter is 13 with all of its corners on the circle. The area of the rectangle is 60. What are the dimensions of the rectangle? Hint: Draw a picture and use the Pythagorean Theorem.

Answer 1

Given

A rectangle is placed inside a circle whose diameter is 13unit all corners of it on the circle.

area of the rectangle = 60 square unit

Find the dimensions of the rectangle.

To proof

As given in the question

rectangle is placed inside a circle whose diameter is 13unit .

now by using the diagram given below

the diagonal of the rectangle is equal to the diameter of the circle.

Thus DB = 13 unit

FORMULA

Area of the rectangle = Length × Breadth

area of the rectangle = 60 square unit

let the value of the length be ( Say AB ) = x

put the value in the above equation

we get

60 = x × Breadth

`Breadth( say AD)= (60)/(x)`

now in ABD

Using the pythagorus theorem

we get

BD²= AB² + AD²

`13^(2) = x^(2)+ ((60)/(x)) ^(2)`

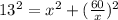
solving the above equation

we get

`169x^(2)= x^(4) + 3600`

`x^(4) - 169x^(2)+3600 =0`

`x^(4) - 144x^(2) -25x^(2) + 3600 =0`

`x^(2) (x^(2) - 144) - 25 (x^(2) - 144) =0`

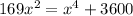
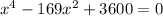
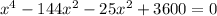
(x² - 25) (x² -144) =0

The roots are

x = -12 ,-5, 5, 12

-12 and -5 are neglected because of negative terms .

( Length and breadth of recangle cannot be negative )

thus x = 12 and 5

Two case arise

First case

when

Length of rectangle= 12unit

`Breadth = (60)/(12)`

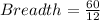
Breadth of rectangle = 5 unit

Second case

Length of rectangle= 5unit

`Breadth = (60)/(5)`

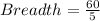
Breadth of rectangle = 12 unit

Hence proved