Question

Calculate midpoint of (8,4) and (12,2)

Answer 1

The formula of a midpoint:

`M_(AB)\left((x_A+x_B)/(2),\ (y_A+y_B)/(2)\right)`

We have:

`A(8,\ 4)\to x_A=8,\ y_A=4\\B(12,\ 2)\to x_B=12,\ y_B=2`

Substitute:

`(8+12)/(2)=(20)/(2)=10\\\\(4+2)/(2)=(6)/(2)=3`

Answer: (10, 3).

Answer 2

Let's first recall what is known as the Midpoint formula we have, so by the Midpoint formula, we know that, the midpoint of any line segment joining the points
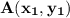`{\bf{A(x_(1),y_(1))}}` and
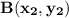`{\bf{B(x_(2),y_(2))}}` is given by

• 
  `{\boxed{\bf{M(x,y)=\bigg((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2)\bigg)}}}`

Now, if we assume our points to be A(8,4) and B(12,2) and the midpoint being M, then we will be having :

`{:\implies \quad \sf M=\bigg((8+12)/(2),(4+2)/(2)\bigg)}`

`{:\implies \quad \sf M=\bigg((20)/(2),(6)/(2)\bigg)}`

`{:\implies \quad \boxed{\bf{M=(10,3)}}}`

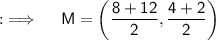
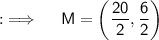
Hence, the required Midpoint is (10,3)