Answer:
d=10 units
Explanation:
Hello.
Step 1
the formula of the distance between two points is based on the Pythagorean theorem, which states that in a rectangle :

Now, suppose we have two points P1(X1,Y1) and P2(X2,Y2), the distance between the two points will be the hypotenuse of our triangle, the difference in x will be the adjacent leg, and the difference in coordinates in y will be our opposite leg.
adjacent side =X2-X1
opposite side=Y2-Y1
hypotenuse=distance between P1 and P2
replacing
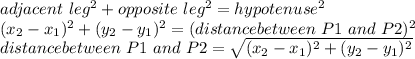
we take only the positive root because it is a distance, a negative distance makes no sense
Step 2
find the distance between A(1,1) and B (7,-7) using the formula
Let
P1=A(1,1)
P2=B(7,-7)
put the values into the formula
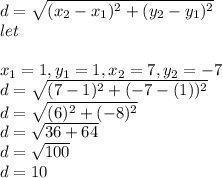
d=10 units
Have a good day.